Darwin's discovery of natural selection as the mechanism of evolution and Mendel's subsequent discovery of the basic principles of heredity led to one of the most remarkable paradigm shifts in the history of science. The mechanism is often paraphrased as "the survival of the fittest" and some of the basic problems, eg the very definition of fitness, are inherently mathematical. Evolution does not, of course, take place in a vacuum. Individuals continuously interact with the environment and the fitness of an individual depends on the environment it experiences. As this environment includes and is influenced by the rest of the individual's conspecifics and competing species, it is clear that evolution is intimately linked to population dynamics.
Adaptive dynamics is a relatively new mathematical theory that explicitly relates evolution by natural selection to ecology, that is, population dynamics. Intensive research on adaptive dynamics is being carried out at the University of Helsinki, the International Institute for Applied Systems Analysis (IIASA) and the University of Liverpool, to name only a few (see links at below). Using this theory one can address and often answer questions such as "When can a rare mutant invade a population?", "Under what circumstances does speciation take place?", "Are there evolutionary attractors?" and many more.
Ecological interactions and population dynamics are modelled as a dynamical system. A population consists of individuals that differ from each other in age, size and other characteristics. The state of the population is the distribution of these characteristics, which is an infinite-dimensional quantity.
In Figure 1 we have plotted a possible bifurcation diagram of a one-dimensional projection of such an infinite-dimensional dynamical system. On the horizontal axis is a bifurcation parameter q and on the vertical axis is the total population size N. Thick lines correspond to stable steady states and dashed lines to unstable ones. The bifurcation from the steady state N=0 corresponding to population extinction is a so-called subcritical or backward bifurcation. In a certain parameter range there is bistability: in addition to the stable extinction state there is another stable steady state corresponding to a viable population.
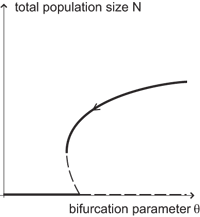
Assume now that the parameter q describes a heritable trait that is subject to natural selection. The invasion fitness of a rare mutant q' introduced into a resident population of individuals of trait q is defined as the long-term exponential growth rate of a (hypothetical) clan of such mutants in the environment set by the resident population. If the invasion fitness of the mutant is greater than zero, then the mutant can invade and possibly replace the resident. We can therefore provide the branches of stable steady states in a bifurcation diagram with an arrow indicating the direction in which the life-history parameter under selection will change in the course of evolution.
In Figure 1 we have assumed that selection favours smaller values of q and have therefore drawn an arrow pointing from right to left on the nonzero branch of steady states. If this is indeed the case, the parameter q will decrease and the steady population size N will follow the thick line until it reaches the tip of the branch. Then, because the arrow (or selection gradient) still points to the left the population will suddenly go extinct (drop to the steady state N=0).
The above scenario is an example of evolutionary suicide. Individuals with smaller q-values do better than individuals with greater q-values and will take over. Eventually this leads to extinction of the whole population. It has been proved that evolutionary suicide is always related to a backward bifurcation of the type depicted in Figure 1. In a forward (supercritical) bifurcation in which the stable steady extinction state bifurcates into a stable nonzero steady state without the intermediate unstable steady state of Figure 1, evolutionary suicide is not possible. In evolutionary suicide the population therefore goes extinct from a relatively high population density. Gradual extinction occurring by a species becoming rarer and rarer has a different mechanism.
Links:
http://www.helsinki.fi/~mgyllenb/addyn.htm
http://www.iiasa.ac.at/Research/EEP/
http://pcwww.liv.ac.uk/~twevans/homepage
Please contact:
Mats Gyllenberg
University of Helsinki, Finland
Tel: +358 9 19151480
E-mail : mats.gyllenberg![]() helsinki.fi
helsinki.fi










