Statistical Physics Algorithms for Traffic Reconstruction

by Arnaud de La Fortelle, Jean-Marc Lasgouttes and Cyril Furtlehner

Concepts and techniques from statistical physics have inspired a new method for traffic prediction. This method is particularly suitable in settings where the only information available is floating car data. We propose a system, based on the Ising model from statistical physics, which both reconstructs and predicts the traffic in real time using a message-passing algorithm.

The idea behind this development is that current models, while suited to traffic reconstruction and prediction on a motorway, have severe drawbacks in other areas. In the first place, the information available is heterogeneous: sensors can be magnetic loops, video cameras or floating car data (the data retrieved and sent by a car to a server). This generates a lot of noise for analysis.

Second, while some existing urban and inter-urban areas have traffic management and advice systems that collect and analyse data from stationary sensors, many do not. This is the case particularly in rural areas, where crashes account for more than 60% of all road fatalities recorded in OECD countries. Hence, the need for a system that can cover these roads is compelling if a significant reduction in traffic-related deaths is to be achieved.

The Stochastic Model
Most current traffic models are deterministic, that is, described at a macroscopic level by a set of differential equations linking variables such as flow and density. Such models are quite well adapted and efficient on motorways where a fluid approximation of the traffic is reasonable. However, they tend to fail for cities or rural roads, since the velocity flow field is subject to much greater fluctuations. These are induced by the nature of the network (presence of intersections and short distance between two intersections) rather than by the traffic itself. This requires a stochastic model.

These considerations have led to a hybrid approach, taking full advantage of the statistical nature of the information. In order to reconstruct the traffic and make predictions, we propose a model – the Bethe approximation – to encode the statistical fluctuations and stochastic evolution of the traffic, and an algorithm – the belief propagation algorithm – to decode the information. These concepts are familiar to the computer science and statistical physics communities, since it has been shown that the output of belief propagation is in general the Bethe approximation.

Traffic is modelled as a binary-valued graph.

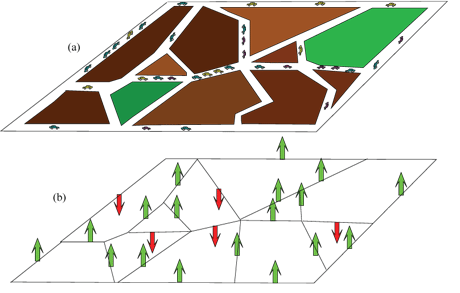
The model is shown in the figure. The network of roads is classically represented as a graph, and traffic state on an edge (a road) is described by a binary value: 0 for fluid and 1 for congested. The important feature of the model is that traffic states are correlated only through the coupling of neighbours. This is the Bethe approximation, a method for finding the exact solutions of certain quantum many-body models. A model such as the Ising model, a simple model used in statistical mechanics, displays a phase transition phenomenon with respect to the value of the coupling. From the point of view of a traffic network, this means that the model is able to describe binary traffic regimes on the whole network: either fluid (most of the spins up) or congested (most of the spins down). This represents the traffic quite accurately: when one part of a road network is congested, it is common that all parts are also congested (and vice versa).

The algorithm used for reconstruction, the belief propagation, reconstructs a Bethe approximation from real data. In fact, the data collected from the probe vehicles is used in two different ways. First, data is collected over long periods in order to estimate the model, ie matching the correlations with historical data. This operation is expensive but can be done once, and updated only if the general behaviour of the network changes. Second, at every period of prediction refreshing (typically five minutes), a reconstruction is performed to match the current data with the model, using the correlations calculated first. This leads both to reconstruction and prediction, since we use a space-time graph.
This algorithm has been implemented, and initial tests using a traffic simulator to generate traffic data show that it is fast (real time for a medium network). The main issue now is stability and precision. The next step is therefore to test it with real data.

Please contact:
Arnaud de La Fortelle
Ecole des Mines de Paris, France
E-mail: arnaud.de_la_fortelleensmp.fr