by Leo Kroon
The Dutch railway timetable for 2007 is probably the only example of high-brow mathematics that is discussed by the whole population of the Netherlands. This timetable is partly based on mathematical optimisation models that were developed by CWI, Erasmus University, and others.
A new railway timetable was introduced in the Netherlands on December 10, 2006. This timetable is cyclic and involves both passenger and freight trains. One hour of the new timetable between the cities Gouda and Utrecht is shown in Figure 1. In this paper we describe several combinatorial optimisation models that were developed for generating cyclic timetables. These models played an indispensable role in the planning process of the new Dutch timetable.
Cyclic Timetable
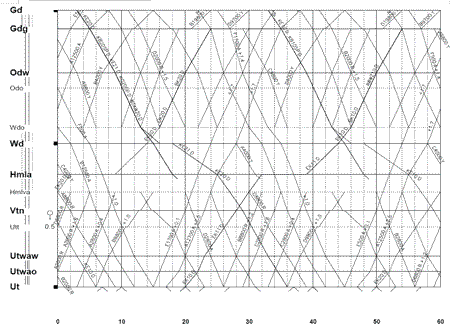
The problem of generating the basic structure of a cyclic railway timetable can be described as a Periodic Event Scheduling Problem. It can be represented by a directed constraint graph, where the nodes are the departure and arrival times and the arcs are the processes between the departure and arrival times.
The Periodic Event Scheduling Problem can be solved by applying constraint propagation techniques. These techniques are adequate if the railway infrastructure is utilized intensively, as is the situation in the Netherlands. In that case, having fixed certain well-chosen parts of the timetable, the remaining solution space for the rest of the timetable is small, resulting in relatively short computation times.
Routing Trains through Stations
In the first timetabling step, the stations are considered more or less as black boxes: the details of the routes of the trains through the stations are considered only in an aggregated way. Therefore, in a second step, it must be checked in detail whether, given the arrival and departure times that were generated in the first step, the trains can be routed through the stations and allocated to platforms.
The problem of routing a set of trains through a station can be solved by first listing for each train the feasible routes through the station. Next, each combination of a train and a feasible route can be represented by a node in a graph. Two nodes are connected by an edge if they belong to the same train, or if the corresponding combinations of trains and routes are conflicting. The routing problem thus reduces to the problem of finding a maximum weighted node packing in this graph.
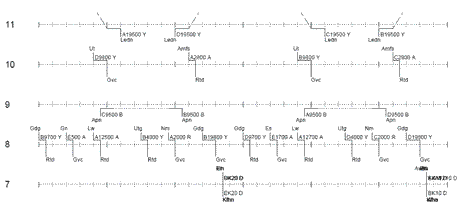
This weighted node packing problem can be solved by applying the commercial mathematical programming optimizer CPLEX, after several pre-processing techniques have been applied for reducing the size of the graph. Figure 2 shows part of the platform allocation chart for Gouda station in the new timetable.
Robustness
In the first timetabling steps, it is assumed that the process times in the timetable are deterministic. However, the real-time process times in the operations are stochastic. The robustness of the timetable against small disturbances can be improved by optimally allocating time supplements and buffer times in the timetable.
This optimisation can be supported by a stochastic optimisation model that considers the processes both outside and inside the stations. The model modifies an initially given cyclic timetable and, at the same time, evaluates the modifications by simulating the trains in the timetable under stochastic disturbances. The aim is to minimize the average delay of the trains. This model can be considered as a symbiosis of an optimisation model and a simulation model.
Conclusions
The models described here were used intensively in the development of the Dutch timetable for 2007. The same holds for the multi-commodity flow model that was developed for planning the corresponding rolling stock circulations and for the set-covering model that was developed for generating the crew schedules.
Altogether, mathematics played an indispensable role in the generation of the new timetable, the rolling stock circulation and the crew schedules. The mathematical models allowed several scenarios to be generated, and explicit trade-offs to be made between conflicting optimisation criteria. This leads to a higher overall quality of the plans, as well as to a reduction of the lead-time of the planning process.
Currently, we are investigating whether these models can also be applied to support real-time control processes. That is, how can plans be adapted in the case of a real-time disruption of the railway system such that the passenger service remains as good as possible? Here the time needed for computing appropriate solutions is more important than near-optimality of the solutions: heuristic methods will be required.
Links:
http://www.ecopt.nl
http://www.cwi.nl/pna1
http://www.ns.nl
Please contact:
Leo Kroon
NS Reizigers, Utrecht and Erasmus University Rotterdam, the Netherlands
Tel: +31 30 2356658 or +31 10 4082421
E-mail: lkroon![]() rsm.nl
rsm.nl










