Anna Gambin, Anna Marciniak-Czochra and Damian Niwinski
Alan Turing’s achievements in the theory of computation led to his recognition as the father of modern computer science. The most prestigious award in the field is named after him. He is also widely recognized in cryptography for his work on “Cryptology bombs” - code-breaking machines that were used by the Allies during the Battle of the Atlantic. Turing’s fascination with the process of thinking has led to the formulation of the definition of an abstract computing machine. By proposing a test to measure the machine’s ability to exhibit human-like cognition and consciousness he initiated the field of artificial intelligence. It is less well known that he spent the last few years of his life developing mathematical theories to describe biological processes.
This year we celebrate the 100th anniversary of Turing's birth and the 60th anniversary of the publication of the seminal work The Chemical Basis of Morphogenesis [1], which provides the basis of the mathematical theory of pattern formation. The Turing reaction-diffusion systems had predicted phenomena such as oscillating reactions, discovered only 10 years after his premature death.
The father of modern computer science not only had an enormous influence on the progress of computation technology - he also benefited from it: while working on morphogenesis and phyllotaxis, Turing used computer simulations to obtain solutions. Modern developments in biosciences provide tools to study molecular processes in living organisms that now are carried out on an unprecedented scale, a continuation of the research initiated by Alan Turing.
If Turing, the boy fascinated by the sophisticated design of a daisy flower on the playing field, were alive today he would have a previously unavailable opportunity to observe and understand nature. Doubtless, he would use the opportunity to reconcile the beauty of mathematics with the truth of life. For this reason, Alan Turing can also be considered to be a forefather of Systems Biology - a new fast-growing field of knowledge based on collaboration between biologists, mathematicians and computer scientists. The essence of Systems Biology, the study of systems ranging over multiple scales (such as impact of signaling pathways on cell division and further on tissue architecture), is embedded in Turing’s theory of pattern formation. The multiscale study of the movement of molecules (idealized as diffusion) has been proven by Turing to contribute to the diversity of patterns in living beings, from amoebae to cnidarians to vertebrates. The implications are wide-reaching.
Next-generation sequencing projects (such as the 1000 Genomes Project) contribute to the understanding of the genetic diversity of the human population. Microarray technologies have become standard in the study of the dynamics of gene expression, both in physiological processes and in disregulated cell signaling pathways. The study of proteins on the proteome scale is made possible by mass spectrometry. New research techniques provide data on the behaviour of objects such as genetic sequences, transcripts, and proteins. Systems Biology seeks to identify the interactions between these objects, which are in turn responsible for complex molecular processes. Analysis of these new data is challenging because of the combined complexity of the structure of the data as well as their size, which necessitates the use of sophisticated algorithmic techniques.
The value of rigorous mathematical modelling of molecular data should not be underestimated. Modelling can save time and money because the system’s behaviour can be tested in silico, followed by a "wet" experiment involving only the most promising scenarios. To sum up, Systems Biology employs a combination of molecular biology, mathematics and computer science. Its main applications are in molecular medicine, but it also has a significant impact on agriculture and biotechnology.
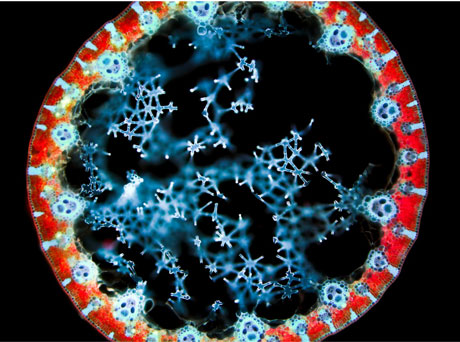
Brandner, D. and Withers, G. (2010) Images of fluorescence micrograph showing the cross-section of bulrush (Juncus sp.) leaf, autofluorescing red (chlorophyll on external side of leaf) and blue (vascular bundles).
Jan Martinek and the 2011 Olympus BioScapes Digital Imaging Competition®.
We recommend the Fundamenta Informaticae Special Issue [2] in which various applications of mathematical theories to natural phenomena, inspired by Turing's work, are considered. The works in the volume represent the latest trends in systems biology research, such as: stochastic and spatial models of molecular processes, self-organizing patterning in the development of higher organisms and state-based modelling.
Nearest to Turing’s classic achievements is the work by Błażewicz and Kasprzak who study computational complexity issues inspired by computational biology. One of the issues they address is the similarities and differences between DNA computers and nondeterministic Turing machines.
A very modern approach to morphogenesis is presented by Setty et al. They describe the state-based modelling of morphogenesis, which results in a fully executable program for the interactions between chemical entities and morphogens. Furthermore, they discuss a variant of the original Turing test of machine intelligence, as a future means to validate computerized biological models.
Interactions of spatial and stochastic effects in a model of viral infection are studied by Bertolusso and Kimmel. Reaction-diffusion systems can be viewed as mean-value approximations of random walk based stochastic systems of interacting molecules.
A mathematical formulation of Driesch and Wolpert's positional information theory of emergence of organization in multicellular organisms is presented by Vakulenko and Radulescu.
Three-dimensional modeling of receptor signaling networks dynamics is a challenge solved in the paper by Archuleta et al. by means of a novel multi-resolution Monte Carlo technique. It allows observation of an interesting mechanism, adaptor protein hopping, that explains the increase in signaling efficiency when receptors are co-located.
The phenomenon of self-organized patterning during development of higher organisms is the focus of the work by Batmanov et al. The paper studies the dynamics of a community effect in space and its roles in two other processes of self-organized patterning by diffusible factors: Turing’s reaction-diffusion system and embryonic induction by morphogens.
References:
[1] Turing, A. M. (1952). The Chemical Basis of Morphogenesis. Philosophical Transactions of the Royal Society of London 237 (641): 37–72.
[2] Watching the Daisies Grow: from Biology to Biomathematics and Bioinformatics -- Alan Turing Centenary Special Issue, (2012) Fundamenta Informaticae.
Please contact:
Ania Gambin
University of Warsaw, Poland
E-mail:
{jcomments on}










