Future quantum computers may use exotic materials which host entirely new types of physical particle, called anyons. Computations in such Topological Quantum Computers would be done by exchanging the anyons, creating 'quantum knots' in the process. This idea has spawned an international effort encompassing pure mathematicians, theoretical and experimental physicists and material scientists. The first electronic devices which are supposed to detect and manipulate anyons have recently been constructed in two-dimensional electron systems, with promising results.
Quantum computers of sufficient size and reliability would not only cause a revolution in data security, but should have many more exciting applications, such as the design of special materials and chemicals. Nevertheless, progress in the fabrication of quantum computers has been slow because in most approaches to quantum information processing, the quantum systems employed to store and manipulate information are very sensitive to noise, either from the environment or due to small errors in controlling the computer's components. This causes these computers to effectively lose their memory - we say there is decoherence of the stored quantum information. Quantum error correction software can in principle solve this problem, but this requires much more reliable basic components than those currently available.
Topological quantum computation (TQC) aims to eliminates decoherence at the hardware level, by encoding quantum information in non-local properties of a suitable quantum system, which cannot easily be disturbed by noise - this is somewhat analogous to the old memory aid of knotting a handkerchief. The information storage and manipulation in topological quantum computers makes use of anyons. Anyons are particles which have the property that the quantum state of the system transforms in a non-trivial way when one of these particles encircles another. As the anyons move around, encircling one another in different ways, their 'world-lines' become tangled up and form knots. To visualize this, we can think of each anyon as connected to a thread and these threads forming a braid as the anyons at their ends are moved around (Figure 1). Systems with sufficiently interesting anyons can reliably store a number of qubits which grows linearly with the number of anyons. The quantum states which make up the qubits can be obtained from some initial state, and also manipulated further for calculation, by 'braiding' the anyons in different ways. Crucially, as long as the temperature is low enough and the anyons are kept well-separated, there is essentially no other way to disturb the stored information, which makes this computation scheme extremely stable against decoherence.
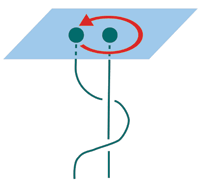
Figure 1: Two anyons in a plane. One encircles the other and the figure shows the braid corresponding to that process.
Anyons can only exist in systems which are effectively two-dimensional, that is, they live in a single plane. Important examples of such systems are two-dimensional electron gases (2DEGs) which can be created on the interfaces between various semiconducting materials, and graphene, a two-dimensional form of carbon which recently earned Andre Geim and Konstantin Novoselov the 2010 Nobel Prize in physics. The most advanced experiments on anyons to date employ 2DEGs at very low temperatures and very strong magnetic fields. Under these conditions the fractional quantum Hall effect occurs - the electrons form incompressible liquids and the smallest possible holes (2D 'bubbles') in some of these liquids are expected to be anyons useful for quantum computation. To experimentally establish the statistics properties of these holes is non-trivial, precisely because these properties are impervious to local probing.

Figure 2: Schematic of a double point contact interferometer, a way to detect and manipulate anyons.
Groups in Maynooth and in the wider Dublin area work on many aspects of planar physics and its application to TQC:
- general mathematical underpinnings of the theory of anyons
- construction and study of exactly solvable microscopic models in which anyons emerge
- numerical study of realistic models, for example for fractional Quantum Hall systems
- interpretations and predictions for concrete experiments.
An important line of research has focused on interferometers like the one pictured in figure 2.
Teams of experimental physicists at Bell labs, Princeton, Harvard, the University of Chicago and the Weizmann Institute have already constructed devices similar to this, and promising evidence for the existence of non-Abelian anyons has been emerging. Microsoft has also poured significant scientific and financial resources into this line of research through its TQC research station, 'Microsoft Station Q'.
The figure shows electric current carried by anyons, flowing along the edges of a 2DEG in the fractional quantum Hall regime (seen from above). In two places, the edges are pushed together using contacts shown as gray rectangles. At these two point contacts, anyons can quantum tunnel from the bottom edge to the top. Current which flows from the bottom to the top thus comes from a quantum superposition of amplitudes to take either the green or the red path. This causes oscillations in the current when the size of the region enclosed by the paths is varied. The gray disc in the figure represents a contact which may be used to vary the number of anyons inside the interferometer. The number of anyons inside the interferometric region can dramatically affect the current; in the very simplest model, the presence of an odd number of anyons makes the current oscillations disappear completely, while an even number of anyons has no such effect. Observing these two behaviors in the same system would be a dramatic signature of the presence of non-Abelian anyons (the kind of anyons needed for TQC). Devices such as this are likely to provide the first smoking gun detection non-Abelian anyons, and also provide an important tool in manipulating the state of future anyonic quantum computers.
Links:
http://www.thphys.nuim.ie/daqist/
http://www.thphys.nuim.ie/staff/joost/PI/intro.html
http://stationq.ucsb.edu/
Please contact:
Joost Slingerland
Department of Mathematical Physics
National University of Ireland Maynooth
E-mail:










