We present modelling and simulations of Bio-FETs (Field-Effect-Transistors), a complex multi-scale system where a semiconductor device is coupled to a bio-sensitive layer that detects bio-molecules such as DNA in a liquid. Our mathematical modelling yields qualitative understanding of important properties of Bio-FETs and helps to provide high performance algorithms for predictive simulations.
Recent experiments have shown the possibility of detecting bio-molecules in a liquid by the effect of their intrinsic charge on the conductance of a semiconducting nano-wire transducer. Such sensor devices are fast, cheap and label-free. Figure 1 shows a schematic Bio-FET, which consists of a semiconducting transducer separated by an insulator layer (typically silicon dioxide or nitride) from the biological recognition element (receptors or probe molecules) that surrounds the transducer immobilized to the surface, consisting of antibodies, proteins, enzymes, nucleic acids or living biological systems. The transducer immerges into an electrolyte (aqueous solution of NaCl) that contains the analyte, i.e. the target molecules that we want to detect, such as DNAs, antigens, proteins. The principle of Bio-FETs is actually simple: when the analyte bio-molecules bind to the surface receptors, the charge distribution at the surface changes, which modulates the electrostatic potential in the semiconductor and thus its conductance which can be easily measured. Since the device detects a specific substance, the change of the conductance yields the concentration in a rather direct way.
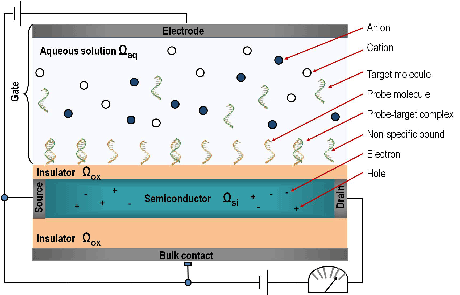
Figure 1: Schema of a Bio-FET sensor.
The modelling of such Bio-FET sensors must take into account the electrostatics and geometry of the liquid, the probe and the target molecules in the boundary layer, the binding efficiency of the probes and targets, the electrostatics and the conductance of the semiconducting transducer and device geometry. Note that the bio-molecular and the nano-electronic part define very different length scales, they have to be considered separately and then coupled in a self-consistent manner.
As a mathematical model for the transport of electrons and holes inside the transducer we use the drift-diffusion equation coupled to the Poisson equation. The standard continuum model is the mean-field Poisson equation, in which the free charges are treated as points, included using Boltzmann statistics. The classical Poisson–Boltzmann theory is successfully used to study the planar electric double layer and the electrolyte bulk.
In our multiscale problem the original Poisson equation is replaced by a homogenized problem consisting of the Poisson equation with two interface conditions at the surface. The values that determine the interface conditions are easily evaluated from the simulations. The boundary conditions for bio-sensors include the selectively adsorbing surface with probe molecules or purely reflective (inert) walls.
A key aspect of the modelling is the calculation of the charge distribution in bio-functionalized surface layers. Both electrostatic and the hard-sphere collisions are sensitive to ion size. Since the electrolyte is usually buffered, it is essential to consider not only mixed-size, but also mixed-valence ionic systems. Therefore the radius and valence of the ions are specified as input parameters.
Since the applied voltage between electrodes and the bulk concentrations of the ions are controlled in experiments, their influence on the ionic concentrations also has to be investigated. The Metropolis Monte Carlo (MMC) algorithm in the constant-voltage ensemble is the appropriate numerical method. We have extended it to investigate the ionic concentrations near the groups of charged objects with various geometries and sizes, representing, for instance, DNA strands in different orientations.
Another crucial aspect of the modelling is the simulation of the transport of target molecules in the analyte solution to the active sensor area. There are several mechanisms:
a) Diffusion. b) Convection. c) in addition, the pump is essential for the fast response times. d) Migration: The movement of charged particles in response to a local electric field. Its contribution to the total flux is proportional to the charge of the ions, the ion concentration, the diffusion coefficient, and the strength of the electric field gradient, which is induced by the ion and by the applied external potential.
The internal electrical potential is obtained via Poisson equation. The velocity field is modelled by the Navier-Stokes equations. Note that diffusivity depends in general on the type (size and shape) of the molecules.
All these processes are taken into account in the algorithms for the diffusion-convection-migration (DCM) problem with chemical reactions near the functionalized surface.
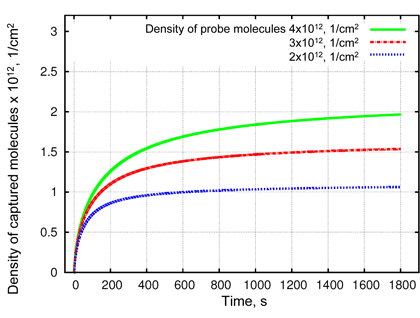
Figure 2: Simulation results of reaction-diffusion problem for density of probe-target complexes obtained at different probe densities. A higher probe density (green lines) leads to a faster binding at the beginning of the simulated process and to a decrease of total analyte concentration in the solution (not shown here). That results in a lower binding efficiency of captured analyte at higher probe density. Thus, at t=1400s the binding efficiency will be 48%, 50%, and 52% for probe densities of 4x1012 (green), 3x1012 (red) and 2x1012 (blue) molecules per cm2, respectively.
The whole simulation consists of different steps as follows:
1) DCM is solved to find a concentration of analyte molecules for every space point at a time.
2) The target molecules, which have reached the functionalized surface, take part in the chemical reactions described by ordinary differential equations for specific and non-specific binding. By solving them we find a distribution as well as binding efficiency of captured molecules. The density of probe-target complexes for varying density of probe molecules is shown in Figure 2 as a function of time.
3) Then the MMC is applied to find the ionic concentrations near the surface and within the intermolecular space. At first the simulation is performed with the surface that is functionalized with probe molecules, which have a known density, and then the MMC is applied to the probe-target complexes with the same density.
4) For coupling atomistic and continuum models, microscopic charge distributions from the MMC solver are recalculated to the macroscopic surface charge densities and to the macroscopic dipole moment densities. They are weighted by the binding efficiency and used as interface conditions in the homogenized Poisson equation.
5) Finally the Poisson equation provides the voltage for MMC and external potential for migration model.
A self-consistent loop between the micro- and macroscopic simulations provides the basis for the quantitative description of BioFETs and their predictive simulation.
Acknowledgement: this work was supported by the Austrian Science Fund (FWF, projects W8 and P20871), the Viennese Fund for Technology and Research (WWTF, project MA09-28) and the European Commission (project MEST-CT-2005-021122 “DEASE”)
Link: http://www.wpi.ac.at
Please contact:
Norbert J Mauser
Wolfgang Pauli Institut c/o Univ. Wien
E-mail:
Clemens Heitzinger
WPI and DAMTP, Univ. Cambridge
E-mail:










