by Michael Mc Gettrick
We are working on features displayed by a number of new scenarios in Quantum Random Walks (QRW).It is expected that many features of QRWs (eg hitting time, localization) will be useful in developing quantum algorithms. Amongst other topics, we look at "memory effects" in walks, simulating a 2-dimensional walk with a 2-state coin, and quantum fairness in lazy QRWs.
In classical Markov models, one of the ways of extending the system is to take in to account the "history" of the previously occupied states. The simplest extension (looking "back" one step) has been studied by us in the corresponding QRW. We get different probability distributions compared to the QRW without history (or, as we call it, memory). In particular, for certain initial states of the Quantum Walker, the phenomenon of localization is observed at the origin: In this case, even after an infinite number of steps, the probability of finding the walker at the origin is greater than 50%. This does not happen in either "standard" QRWs or indeed in classical random walks. The techniques we employ are both rigorous mathematical calculation, and simulation by "running" a finite number of steps of the walk on a computer. We have found the simulation often suggests features of the walk that we can then try and prove. This work is all carried out in the De Brun Centre for Computational Algebra at the National University of Ireland, Galway.
In a further project, we look at QRW with memory on the Cayley Graph of an Abelian Group. This is collaboration with Claas Roever (Galway), Mike Batty (Durham) and Jaroslaw Miszczak (Polish Academy of Sciences). We have had some successes here with analysing the simple case of the QWR on a cycle (which is a Cayley Graph of the cyclic group). When we add one step memory to this, it becomes a QRW on a Cayley Graph of the Dihedral Group. The aim is now to understand the general picture of re-writing a QRW with memory as one without memory on a different graph. One of the reasons we carry this out is we believe putting in memory in to the process gives us a type of control over the probabilistic outcomes that could be useful in directing algorithms.
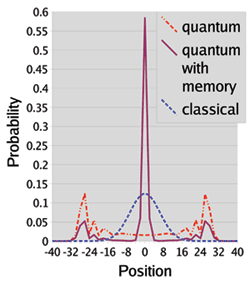
Figure 1: A plot of the probability distributions in a Quantum Random Walk with memory on the straight line (purple). For comparison, the classical walk (blue) and Quantum Walk without memory (red) are also shown. The number of steps in this walk is 40. The walk with memory shows the feature of localization, with over 50% of the probability at the origin.
Work in collaboration with Carlo Di Franco and Thomas Busch at University College Cork has focused on how we can decrease the resources needed to construct QRWs in 2 dimensions. Taking the typical square lattice as an example, we have successfully constructed the Grover Walk without using a "2 dimensional coin". Our walk uses simply a 2-state coin, but alternates the moves up/down and left/right to get 2-dimensional behaviour. The Grover walk comes from the same ideas as used in the famour Grover Algorithm for searching an unordered list. Because our walk uses a lower dimensional coin, we expect it to be easier to implement in a physical scenario. We hope soon to be able to extend the idea of an alternating walk to other models.
Finally, along with research students David Dolphin and Aine Ni Dhonnacha at NUI, Galway, we have looked at the idea of Lazy QRWs, and have phenomenological results in this area. Our idea has been to use the 3 state qutrit to model the 3 possibilities in a lazy QRW (move left, move right, stay put). A further online quantum walk simulator has been built (see URLs at the end) to simulate QRWs on the cycle.
Links:
http://www.maths.nuigalway.ie/~gettrick/research/
http://walk.to/quantum
Please contact:
Michael Mc Gettrick
National University of Ireland, Galway
E-mail:










