by Marlene Müller
The financial mathematics department at the Fraunhofer Institute for Industrial Mathematics (ITWM) covers all important topics of modern financial mathematics which has been an extremely innovative research area during the last years.
The underlying mathematics is often new and at the same time very sophisticated, due to the complex structure of the modelling process. Financial mathematicians need to be familiar with stochastic processes, stochastic calculus and partial differential equations, as well as parametric and non-parametric statistics. The Financial Mathematics Department at the Fraunhofer Institute for Industrial Mathematics (ITWM) covers all the important topics of financial mathematics, in particular:
- option pricing using stochastic and local volatility models
- continuous-time portfolio optimization
- credit risk, Basel II, valuation of credit derivatives
- asset liability management, insurance mathematics, Solvency II.
In addition, risk management as an overall topic complements these more specific areas:
Option Pricing with Stochastic Volatility Models
Options are financial products with a price that depends on the price dynamics of one or several underlyings. A simple example is stock prices following a geometric Brownian motion and leading to the famous Black-Scholes formula for simple call or put options. Various other underlyings are possible, which include not only bonds, interest rates, commodities, exchange rates and investment funds, but also weather observations or CO2 emissions.
Option pricing is one of the most popular fields in financial mathematics. Option trading is an important issue, particularly when market conditions are unfavourable. In order to hedge risks and to offer investors attractive products with a limited risk of loss, banks offer all kinds of derivatives with complex payoff structures; such as products with minimum capital guarantees or products that limit the gain via an upper bound. To calculate precise and market-conformal prices for such derivatives, it is necessary to choose a flexible and appropriate stochastic model for the underlying prices.
A popular generalization of the Black-Scholes model is the Heston (1993) stochastic volatility model. To calculate the price of a complex derivative as a discounted expected value of the payoff (under the risk-neutral measure), appropriate numerical methods (tree approaches, Monte Carlo, PDE methods) must be used. The price calculation is often complemented by the calculation of the Greeks, the sensitivities of the price to various model parameters.
The Fraunhofer ITWM has implemented the Heston model within an integrated option pricing software framework. Due to closed-form solutions for standard calls, this model offers a time-efficient calibration of the model parameters to actual market situations. In addition, the Heston model has the ability to reproduce the volatility smile observed in, for example, stock markets.
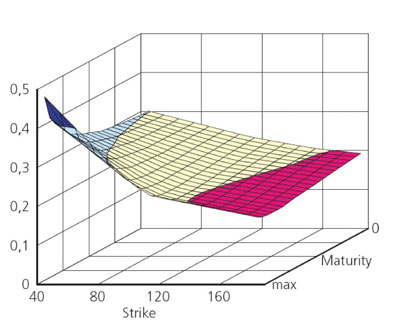
Credit Risk: Basel II and Credit Derivatives
Modelling of credit risks has been an important issue in recent years, for two reasons. The first is the implementation of the new capital regulations (Basel II) and their evaluation by the banking supervision, which is essentially completed now for many banks. The second is the development of several types of credit derivatives that have allowed banks to give away part of their credit risk. (This led to the subprime credit crisis and eventually also the current financial crisis.)
The Fraunhofer ITWM supports banks in their implementation of the Basel II regulations by providing expert knowledge in statistics, gained over the course of several successful research and consulting projects. A typical task is to assess the rating system from a statistical point of view, which means assessing the discriminatory and predictive power of the scoring method, possibly recalibrating the rating system, and validating specific terms, in particular score weights, default probability estimates or the estimated loss distributions. From a mathematical point of view, the main methods that we apply are classification and regression approaches with a special focus on the specific restrictions required by a rating system. In particular, the rating scores should be parametrically specified, additive and monotonic functions of the underlying risk factors, in order that their specification might be extrapolated to rating segments with no or few credit default observations.
In the field of credit derivatives, many standardized products have been developed during the last few years. An example of such a standardized product based on only one underlying subject is the so-called credit default swap (CDS). The attractiveness of this product comes from the fact that it allows the protection buyer to insure against losses due to credit default of the underlying entity. CDSs are traded not only for large corporations but also for banks and sovereign states, which typically have very low default risk. When CDSs are traded on a sufficiently liquid market, their market prices can be used to calibrate a debtor's default probability (even if an assessment on the basis of historical data is almost impossible).
In addition to single-name-based CDSs, there are more complex types of credit derivatives that depend on several underlyings. Examples of these products are first-to-default swaps (FtD), Nth-to-default swaps (NtD), or the (now rather infamous) collateralized debt obligations (CDO). The valuation of these complex products places a significant demand on mathematical modelling and economical and financial knowledge, since existing models have not been able to characterize the market efficiently. In several research and consulting projects, the Fraunhofer ITWM has dealt with the implementation (particularly with the help of copula approaches) of different models for credit derivatives.
Continuous-Time Portfolio Optimization
Continuous-time portfolio optimization (ie the determination of optimal investment strategies in continuous-time models) is one of the main research areas of the Fraunhofer ITWM. It is one of our goals to demonstrate that such modern portfolio optimization methods can be applied to real-world problems (including transaction costs, nonlinear goods and worst-case bounds), and outperform the simplistic but still widespread one-period Markowitz mean-variance approach.
Asset Liability Management, Insurance Mathematics, Solvency II
Asset liability management (ALM) forms an important part of running a company (especially a bank or insurance company), and it is usually company policy to carry it out regularly. The interdependence between assets and liabilities is about to become even more important, as Basel II (for banks) and Solvency II (for insurance companies) are now being implemented on national and international levels.
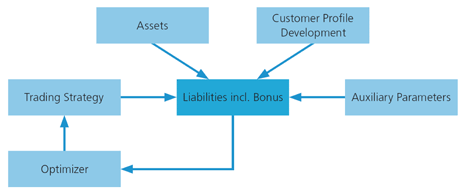
The Fraunhofer ITWM has developed the ALMSim simulation software tool to address this problem. Assets and liabilities can now be modelled individually with client-specific interdependences incorporated. ALMSim has already been used successfully by two pension funds. The software obtains the simulation model from a user-defined input file (ALMSim comprises an intuitive simulation language, very close to mathematical formulae), and then automatically recognizes and resolves logical model dependencies. ALMSim will then simulate the model using the appropriately chosen Monte Carlo methods and discretization step sizes. This enables a user (possibly without programming skills) to adapt the ALM simulation model as required. Model parameters, starting values and results are saved in ASCII format (.csv) such that input data can be imported from Excel, R/S-Plus, Matlab etc, and the results can be exported to these programs where they can be further processed and evaluated.
Link:
http://www.itwm.fraunhofer.de/en/fm/ indexfm/
Please contact:
Marlene Müller
Fraunhofer ITWM Kaiserslautern, Germany
E-mail: marlene.mueller![]() itwm.fraunhofer.de
itwm.fraunhofer.de










