by Jacek Jakubowski and Andrzej Palczewski
Modelling fixed income securities and managing risk in their portfolios is a challenging mathematical task requiring models with an infinite number of risk factors. We have designed new methods of dealing with the risk of defaultable bonds and risk diversification in large bond portfolios.
The Financial Mathematics Group at the University of Warsaw was created in the early 1990s, when a group of mathematicians at the university became interested in financial mathematics. One of the main research interests of the group members is the modelling of fixed income derivatives and the optimization of bond portfolios. Fixed income markets are in certain aspects more complicated than stock markets due to a strong correlation between instruments. There is also no widely accepted 'standard' theory for all interest rate instruments.
Credit Risk
Investment opportunities in fixed income markets include both default-free and defaultable instruments. To model the credit risk of defaultable bonds, one relates the probability of default to the rating class of the issuer (rating classes reflect a firms economic standing). To manage the financial risk of defaultable instruments, it is important to model not only asset prices in every rating class, but also a credit rating migration process. Investigations by our group are concentrating on a bond market model: this has a finite/infinite number of sources of randomness in the Heath-Jarrow-Morton (HJM) framework, driven by Lévy processes admitting discontinuous trajectories. The importance of models with an infinite number of risk factors has been stressed in recent papers, eg Carmona & Tehranchi, Ekeland & Taflin, Cont). In the model containing default-free and defaultable bonds with rating migrations driven by a Markov chain, we have found no-arbitrage conditions (generalized HJM conditions) for all basic types of recovery. This model has been further extended by defining a new class of stochastic processes: F-doubly stochastic Markov chains, used to model credit rating migrations. The extended model is used to valuate defaultable claims. The advantage of the new approach is twofold. First, the known two-state analysis of default/no-default is extended to a multi-state case. Second, we give a pricing formula for defaultable rating-sensitive claims in terms of characteristics of the rating migration process.
Optimal Investments in Bond Portfolios
The construction of a good combination of financial instruments involves an optimization problem: select the best investment portfolio from all admissible portfolios. The seminal paper by Markowitz formulates this as a risk-return trade-off. In its original formulation, it is in fact a mean-variance (MV) optimization, with the mean as a measure of return and the variance as a measure of risk. To solve this problem, it is necessary to know the distribution of random returns of risky assets. The solution procedure is then executed under the implicit assumption that we know both the mean and the covariance matrix. In fact, this assumption does not hold, and the estimation of the mean and covariance is an important part of the solution of the optimization problem.
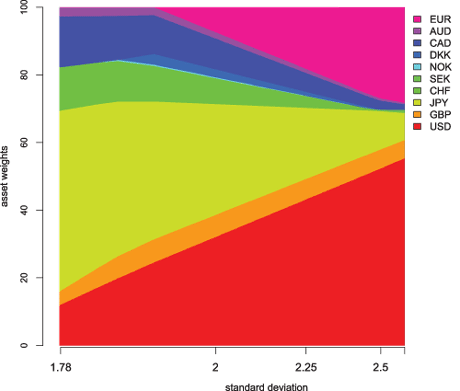
Members of the Financial Mathematics Group have collaborated with an industrial partner to design an optimization method that uses a reasonable set of market data and produces 'good' optimal portfolios, ie portfolios that are well diversified and have asset shares that are stable with respect to estimation errors. The group has had an interesting experience in the optimal tactical asset allocation for a multi-currency bond portfolio. As mentioned above, the main difficulty in implementing MV optimization is the estimation of parameters. While the existing literature points to the difficulty in estimating mean returns, this problem has been overcome using the Black-Litterman method. Our experience shows that the estimation of the covariance matrix is also a difficult task. Standard maximum likelihood estimators lead to unstable portfolios that are sensitive to small changes in data. In order to improve the portfolio stability we apply robust estimators (MCD-type estimators) and implement methods that account for a memory effect in the data. We have also performed a theoretical analysis of the sources of instabilities, and concluded that they are mostly due to small eigenvalues of the covariance matrix. Although this finding is not in itself a surprise, the extent of the instability incurred by small eigenvalues has exceeded our expectations. No remedy could be found in improved estimators; rather, the solution to the portfolio stability issue is to modify the objective function by adding a penalty term of a transaction cost type.
Link:
http://mathfinance.mimuw.edu.pl
Please contact:
Jacek Jakubowski
University of Warsaw, Poland
Tel: +48 22 5544 538
E-mail: J.Jakubowski![]() mimuw.edu.pl
mimuw.edu.pl
Andrzej Palczewski
University of Warsaw, Poland
Tel: +48 22 5544 467
E-mail: A.Palczewski![]() mimuw.edu.pl
mimuw.edu.pl










