Fundamental Modelling of Financial Markets

by László Gerencsér, Balázs Torma and Zsanett Orlovits

In modelling stock prices, two competing approaches exist: technical modelling and fundamental modelling. Technical models capture statistical phenomena observed directly in stock prices, while fundamental models consist of mathematical descriptions of the behaviour of economic agents that affect the stock price. Fundamental models incorporate minute details of the price generating process, and are thus more authentic than technical models. The development and analysis of multi-agent fundamental models has been the subject of research in the Stochastic Systems Research Group of SZTAKI since 2006.

Our model of market microstructures consists of various trading agents, and a stock exchange with order processing rules analogous to real exchanges such as the New York Stock Exchange. The agents observe the market price process, and determine the limit price and order amount in each trading period according to their trading strategy. Agents also consume or invest money. In combination, this gives us a nonlinear stochastic feedback system as the mathematical model, with the stock exchange playing the role of the plant, and the agents playing the role of controllers.

Stock trading literature led us to identify three types of behaviour for trading agents. Trend followers act aggressively in the direction of the current price momentum, meaning they buy more if prices rise sharply and sell when prices fall. Mean reverters take the opposite action to trend followers in the hope that the stock price reverts to some mean value. Fundamentalists develop a belief about the correct price according to the information they receive; they then buy if the observed price falls below this level, and sell otherwise. The believed price process is itself generated by a stochastic price model, which they expect to adequately describe the value of a company.
According to well-known findings in behavioural finance, real traders tend to divert from their trusted trading strategies according to some random pattern. Randomness is also introduced when announcements or news about a company trigger analysts to pay more attention to that company and thus change its valuation. This in turn results in further analysts announcements about that company. This phenomenon can be represented mathematically using self-exciting point processes, which are incorporated in our model.

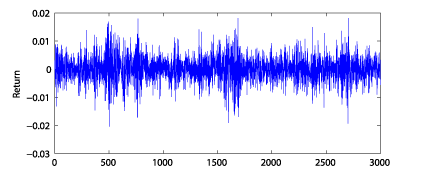
To validate our fundamental model we analysed the volatility characteristics of the generated stock price process using a widely accepted technical model, the so-called Generalized Autoregressive Conditional Heteroscedasticity (GARCH) model. This model generates volatility via a stochastic, nonlinear, Wiener-Hammerstein feedback system, driven by log-returns. This model nicely captures a known volatility clustering phenomenon, as shown in Figure 1 using simulated data.

In fitting a GARCH model we relied on a preceding PhD reseach project on the statistical analysis of GARCH models, in particular the real-time estimation of its technical parameters. The theoretical basis of this work was the highly nontrivial application of an advanced theory of stochastic approximation allowing Markovian dynamics in the underlying state process. We have also developed a highly efficient numerical method for off-line estimation that improves the efficiency of the corresponding module of the MATLAB GARCH toolbox by a factor of 4.5. Simulations have shown that our fundamental model successfully reproduces the volatility properties of price processes generated by GARCH models.

An interesting research topic that we investigated is to analyse the relation between the structure of the artificial stock market and the price volatility; ultimately this was captured by fitting a GARCH model. The market structure is defined and parameterized by the relative weights of agents. These are calculated by dividing the number of agents of any of the three types given above by the number of all agents on the market. All agents are assumed to have the same initial endowment, so relative weights can be seen as the initial distribution of wealth among different groups of agents of a given type. In particular, we investigated the problem of detecting abrupt changes in the market structure, which may be an indicator of insider trading.

Figure 1: A simulated GARCH(1,1) process.

We have carried out extensive experiments in which we simulated stock price time series for different relative agent weights, and then fitted a GARCH model. The parameters of fitted GARCH models are highly dependent on the agent weights, as shown in Figure 2 for the case of GARCH(1,1) models with just two parameters. We indicate the relative weights of mean reverters and trend followers on the x and y axes respectively. Thus each box in the figure corresponds to a relative weight setting, defining a market structure. Shades of grey indicate the range of values of one of the two coefficients of the fitted GARCH model: the lighter the shade the higher the coefficient. This is known as a heat map. The figures above indicate a high correlation between agent weights and GARCH parameters. Using simple technical arguments, Figure 2a indicates that an increase in the relative weight of trend followers increases the volatility. Similarly, Figure 2b can be interpreted as saying that an increase in the relative weight of fundamentalists also increases the volatility. Both of these findings are in agreement with intuition.

We conclude that fundamental modelling of stock price processes is a realistic alternative to the widely used GARCH models. Given the advanced mathematical technology that is currently available to analyse stochastic, non-linear, Wiener-Hammerstein feedback systems we think our approach has great potential for future research in problems such as market stability and robustness.

Please contact:
László Gerencsér
SZTAKI, Hungary
Tel: +36 1 279 6138
E-mail: gerencsersztaki.hu