by Balázs Csanád Csáji, András Kovács and József Váncza (MTA SZTAKI)
One of the key problems in renewable energy systems is how to model and forecast the energy flow. At MTA SZTAKI we investigated various stochastic times-series models to predict energy production and consumption, and suggested an online learning method which can adaptively aggregate different forecasts while also taking side information into account. The approach was demonstrated on data coming from a prototype public lighting microgrid containing photovoltaic panels and LED luminaries.
The presented research was motivated by the E+grid project which aims at building an energy-positive public lighting microgrid using photovoltaic panels, LED luminaries that regulate their lighting levels based on motion sensor signals, energy storage, various sensors and smart meters, wireless commination and a central controller (see Figure 1). A prototype system was developed by an industry-academy consortium formed by GE Hungary, the Budapest University of Technology and Economics, and two institutes of the Hungarian Academy of Sciences (MFA and SZTAKI). The physical prototype, containing 191 luminaries and 152 m2 of PV panels, is located in Budapest at the campus of the MFA Institute of the Hungarian Academy of Sciences [1].
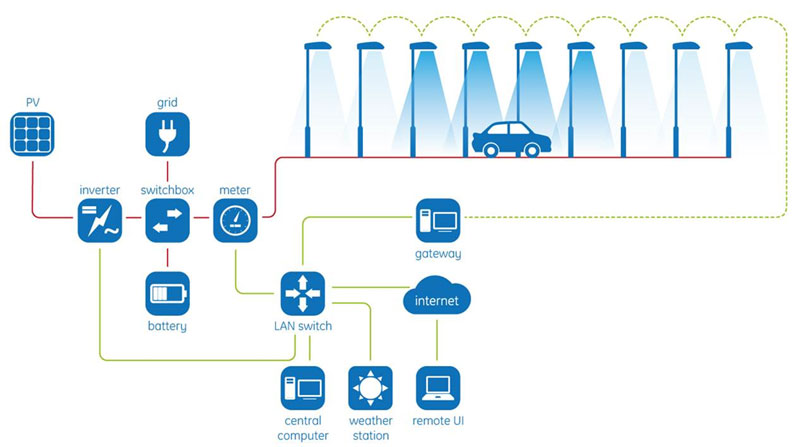
Figure 1: Architecture of the E+grid lighting system.
Stochastic Models of Energy Flow
A crucial problem in renewable energy systems is to model energy flow. It is a challenging task, as both energy production and energy consumption are affected by various external factors, and hence, highly uncertain and dynamically changing. On the other hand, such models are needed to generate forecasts and to build efficient controllers. Several models have been suggested for this in the past, including clear-sky models (i.e., an estimate of the terrestrial solar irradiance under the assumption of a cloudless sky based on astronomic calculations), persistence approaches, autoregressive models, neural networks, fuzzy and hybrid models [2].
During the E+grid project we experimented with a number of time-series models and, after suitable preprocessing (such as removing outliers, noise reduction and normalisation), fitted separate dynamic models to the energy production and consumption processes. We used discrete-time stochastic models with one hour as the time step. The applied models can be classified in two groups: linear and nonlinear. The linear models were: FIR (finite impulse response), AR (autoregressive), ARX (autoregressive exogenous), ARMA (autoregressive moving average), BJ (Box-Jenkins) and state space, while the nonlinear models were: HW (Hammerstein-Wiener), Wavelet, MLP (Multilayer Perceptron), MLPX (MLP with exogenous inputs), SVR (Support Vector Regression) and SVRX (SVR with exogenous inputs) [2].
For the models with exogenous components, we supplied side information as the inputs to help, for example, to cope with the quasi-periodic nature of the problem as well as to provide the available background knowledge on the modelled phenomenon. Side information included the clear-sky prediction for the case of photovoltaic energy production, while it was the typical consumption pattern (based on historical data) for the specific hour of the day, in case of consumption.
After the models were identified, the innovation (noise) sequences driving the processes were estimated. Based on the process and the noise models, forecasts were made by Monte Carlo methods. In the E+grid system, 24-hour forecasts were generated hourly and were used by a receding horizon controller [1].
Online Learning for Context Dependent Forecast Aggregation
While experimenting with various stochastic models we observed that there was no uniformly best model; some models performed better in some situations but worse in others. Since generating forecasts with the already estimated models is computationally cheap, we decided to use all of the models and aggregate their predictions online, based on their past performances in similar situations.
For online learning the best forecasts, we applied the framework of prediction with expert advice. In this framework a learner sequentially faces the problem of predicting an unknown environment based on the predictions and past performances of a pool of experts. The learner aims at minimising its regret, i.e., the difference of its cumulative loss compared to that of the best performing expert so far. The loss is typically defined as the distance between the predicted and actual outcomes of particular variables in the environment. A standard and widely used aggregation rule to combine the predictions of the experts based on their past losses is the exponentially weighted average forecaster (EWAF) [3].
In our case the experts were the estimated time-series models based on which the forecasts were generated. We refined the standard framework by taking contextual information into account as well; namely the losses were weighted by a suitably defined similarity kernel which described how similar the current situation was to the past one in which the expert (the stochastic model) incurred the loss. We also applied discounting to help focus on recent events (e.g., losses incurred a long time ago had lower weights). In addition to the similarity and temporal weighting, our approach, called the state dependent average forecaster (SDAF) was similar to EWAF, e.g., exponential weighting was applied [2].
Experimental Results and Conclusions
Several numerical experiments were performed on the energy production and consumption data coming from the prototype E+grid system [2]. Our results indicate that the applied time-series models, especially the ones using side information, can be efficiently applied to forecast the energy flow in the system. They also demonstrate (see Figure 2) that aggregated approaches can provide better forecasts than single time-series models in themselves. Furthermore, they show that our context dependent aggregation approach (SDAF) outperforms the standard context independent EWAF for this kind of prediction problems.
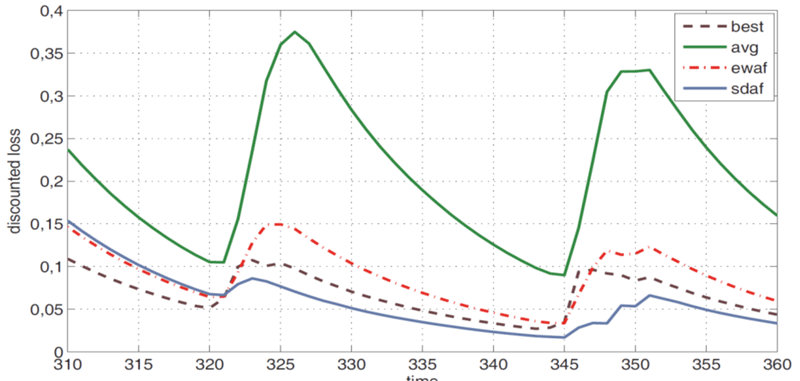
Figure 2. Discounted cumulative loss of predicting photovoltaic energy production for the best, the average, the exponentially weighted average and the state-dependent exponentially weighted average forecaster.
This work has been supported by the Hungarian Scientific Research Fund (OTKA), projects 113038 and 111797. B. Cs. Csáji acknowledges the support of the János Bolyai Research Fellowship No. BO/00217/16/6.
References:
[1] A. Kovács, R. Bátai, B. Cs. Csáji, P. Dudás, B. Háy, G. Pedone, T. Révész, and J. Váncza: “Intelligent Control for Energy-Positive Street Lighting”, Energy, Elsevier, Vol. 114, 2016, pp. 40–51.
[2] B. Cs. Csáji, A. Kovács, and J. Váncza: “Adaptive Aggregated Predictions for Renewable Energy Systems”, in Proceedings of the 2014 IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning (ADPRL 2014), Orlando, Florida, Dec. 9-12, 2014, pp. 132-139.
[3] N. Cesa-Bianchi, G. Lugosi: “Prediction, Learning, and Games”, Cambridge University Press, 2006.
Please contact:
Balázs Csanád Csáji
MTA SZTAKI, Hungary
+ 36 1 279 6231











