by Pieter van den Berg, TU Delft, Guido Legemaate, Amsterdam Fire Department, and Rob van der Mei, CWI
In life-threatening situations where every second counts, the timely arrival of firefighter services can make the difference between survival and death. Motivated by this, the Stochastics Department at CWI in collaboration with the TU Delft and the Fire Department Amsterdam-Amstelland in the Netherlands have developed a mathematical programming model for determining the optimal locations of the vehicle base stations, and for optimally distributing the different firefighter vehicle types over the base stations. Extensive analysis of a large data set for the Amsterdam area demonstrates that, and how, response time can be improved by relocating only few base locations and redistributing different vehicle types over the base locations.
The Dutch capital Amsterdam was the first city in the Netherlands with a professional fire service, which was established in 1874. With 144 personnel and nine fire stations covering 30 square kilometres, it ensured fire protection for approximately 285,000 inhabitants. Today, it is the regionally organized fire department Amsterdam-Amstelland that, with 1,150 personnel and 19 fire stations covering 354 square kilometres, is responsible for over 1,000,000 inhabitants. Obviously, over time the questions of how many fire stations were needed for a given coverage and where to locate them had to be answered numerous times as new needs and means for fire protection emerged.
In this study, we introduce a model to (1) determine optimal locations for the fire stations, and (2) to find an optimal distribution of the vehicles over the selected locations.
We divide the region into a set of demand points from which calls can arise, and define a subset of locations that can be used as a potential base location. We consider different types of vehicles that are used for a different type of call. Each type can have different response time targets. We limit the number of vehicles that we may use of each type. For each demand point and for each vehicle type, we have a weight that indicates the importance of covering a certain demand point by a vehicle of a specific type. The expected number of calls is commonly used for the weights, but other risk measures could be included as well. To determine the coverage, we introduce a subset of the base locations that contains all locations that are sufficiently close to cover our demand point by the specific vehicle. Whether a base location is close enough depends on three variables: the travel time from the base to a location, the pre-trip delay, and the response time target. We assume that the travel times are the same for each vehicle type and that the pre-trip delay, which is the time elapsed before the vehicle starts driving to the scene, is fixed. This pre-trip delay also consists of two parts: (1) triage and dispatch, and (2) chute time. The triage and dispatch time is the time spent in the call centre to assess the importance of the call and assign a vehicle. The chute time is the amount of time that elapses between the assignment of a call and the crew’s departure from the base. The response time target can differ for each vehicle type and for each demand point. For our model, the goal is to maximize the number of calls that are covered by the appropriate vehicle type, while minimizing the number of base locations used [3].
To apply the model to the region of Amsterdam, we defined a set of 2,643 demand points and 2,223 potential base locations. Travel times between potential base locations and demand points are provided by the fire department and are based on estimated travel times on the road network between each location. In our analysis, we include the four most common types of vehicles used at Dutch fire departments: fire apparatus (FA), aerial apparatus (AA), rescue apparatus (RA) and marine rescue units (MR), see Figure 1 for an illustration of the different vehicle types.

Figure 1: Overview of different types of firefighter vehicles: fire apparatus (top left), aerial apparatus (top right), rescue apparatus (bottom left) and marine rescue units (bottom right). Photos: Jeffrey Koper.
The number of available vehicles of each type is respectively 22, nine, three and two. In the current configuration, we have 19 bases. We take the absolute number of calls per vehicle that occurred in 2011 to model the recurring risk. In this period, the number of calls per vehicle type is 29,016, 9,182, 615 and 703, respectively. As an illustration, Figure 2 shows a fictitious relocation of four fire stations.
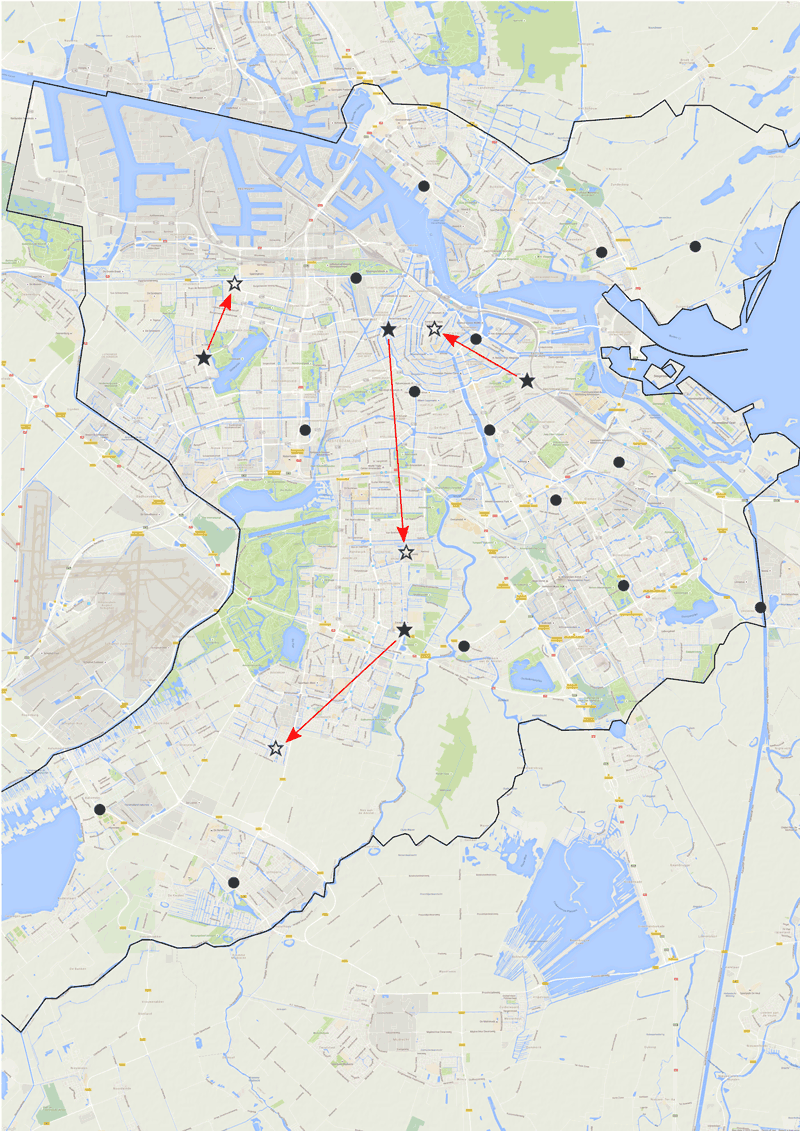
Figure 2: Possible distribution of fire departments where four movements are allowed. Source: G.A.G. Legemaate.
Extensive analysis of a large dataset of historical incidents demonstrates:
- that, and how, a response time can be improved by simply relocating only three out of 19 base locations and redistribution of the different vehicle types over the base locations;
- that there is no need to add new base locations to improve performance: optimization of the locations of the current base stations is just as effective.
The results show an enormous potential for improving the arrival time for firefighter services worldwide. Furthermore, because relocating existing base locations might be considered costly, with only minor adaptations the model can also be used to relocate fire trucks and personnel to temporary locations during large scale incidents to improve coverage.
Link: http://repro.project.cwi.nl
References:
[1] P. Kolesar, W.E. Walker: “An algorithm for the dynamic relocation of fire companies”, Operations Research 22 (2), 249-27, 1974
[2] A.J. Swersey: “A Markovian decision model for deciding how many fire companies to dispatch” Management Science 28, 352-365, 1982
[3] P.L. van den Berg, G.A.G. Legemaate, R.D. van der Mei: “Boosting the responsiveness of firefighter services by relocating few base stations in Amsterdam”, 2015. Under review (a preprint available from the authors upon request)
Please contact:
Rob van der Mei
CWI, The Netherlands
Pieter van den Berg
TU Delft, The Netherlands
Guido Legemaate
Fire Department Amsterdam-Amstelland, CWI, The Netherlands









