by Ulrich Schimpel and Stefan Wörner, IBM Research
Interwoven production lines may be complex, with variable yield and production times, various sub-components competing for processing capacities, and fixed batch sizes. Furthermore, inventory costs need to be minimized and fluctuating customer demands need to be satisfied 98 % of the time. Such complex production lines need to be optimized using a combination of techniques. We describe an approach using a simplified mathematical model that allows for sensitivity analyses, followed by a discrete event simulation to adequately represent the complex business environment.
In supply chain management, there exists a fundamental principle: A better visibility of your supply network processes increases their velocity and reduces their variability [1]. This principle is of increasing importance to successfully operate supply chains in today’s fast-paced world. Imagine you run a manufacturing network with assembly locations world-wide that produces hundreds of products, each requiring dozens of components - also referred to as “bill of material” (BOM) (Figure 1). The target is to fulfil customer demand 98% of the time despite a significant fluctuation in demand, production times, lead times and yield. Achieving this target becomes especially tricky in an environment of multi-purpose resources that are being shared among a set of different products and thus the variability of one product affects a multitude of other products.
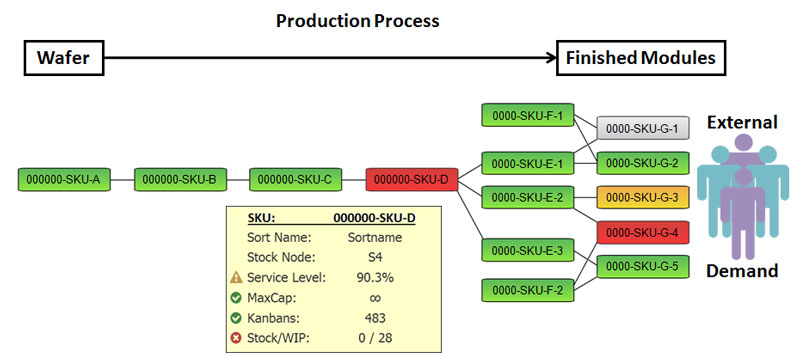
Figure 1: A typical bill of material with colour-coding in the semi-conductor industry for a set of finished goods (right) being produced from a single wafer (left).
The challenge
The described scenario is a daily reality for many companies. One option is to eliminate most variability and waste by well-known concepts such as just-in-time (JIT). However, this is not feasible in environments with a strong inherent variability of individual processes or very long lead times. Also, the business complexity usually inhibits a precise holistic formulation and finding a globally optimal solution. Over the past decade, the authors have been developing feasible approaches for exactly such situations in the semi-conductor industry [2].
A usual primary objective is the satisfaction of delivery times and quantities of all products. A common secondary objective is the minimization of inventory of items required for production lines. Important constraints are “capacity groups” of products that share the available time-variable capacity. It might be necessary to build products ahead of time to avoid a bottleneck capacity in the future. This decision is complicated by existing uncertainty. An opposing constraint on pre-building is the “inventory budget” that must be met at the end of each quarter for accounting reasons. This usually results in splitting or delaying purchases, such that the inventory is likely to hit the accounting books shortly after the next quarter begins. Other aspects to be considered are business rules, lot-sizes, and quantity-dependent stochastic yields. Both of the latter tend to magnify the variability throughout the supply network, starting from the customers. This is known as the “bull-whip effect”
The solution approach
Lacking exact solutions for such an environment, the authors apply a combination of two different techniques. First, a simplified mathematical model is solved which allows for sensitivity analyses. Second, a discrete event simulation evaluates the result from the simplified model in a close-to-reality business context.
The analysis starts with capturing the historical data including all its variability and errors. After cleaning the data, percentiles are derived for the stochastic lead times, and several possible demand scenarios are generated. These demand scenarios can easily be illustrated by their average and extreme instances for evaluation and reporting purposes as shown in Figure 2.
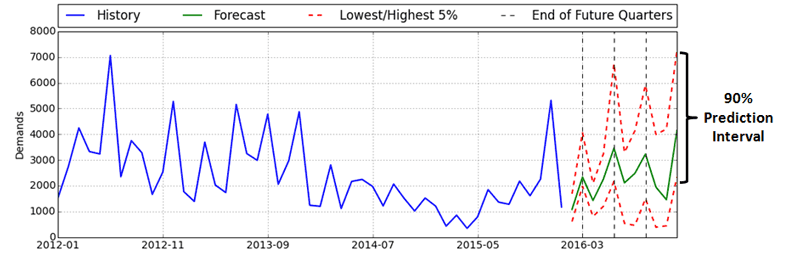
Figure 2: Range of expected demand scenarios originating from stochastic customer behaviour (average and extreme upper / lower predictions).
All data is fed into the mathematical model, which is processed by optimization software to obtain the optimal solution for this simplified setup. It does not help to obtain a fixed schedule, since the stochastic reality will invalidate such a static solution instantly. It is essential to determine an executable policy that is able to react to the concrete situation and that is robust in achieving good results even in the presence of variability. Applying those policies in combination with a periodic re-run of the entire process proves to be a powerful mechanism for volatile environments. The optimization also allows sensitivity analyses to be performed, which identify the bottlenecks that are most prohibitive for obtaining a better result - i.e. a higher service level or lower inventory - in the different capacity groups and over time. This information is valuable since even minor adjustments often lead to significant improvements but are very hard to determine owing to complicated network effects. In Figure 3, the red horizontal limits in periods 1, 2, 5, and 6 indicate critical bottlenecks in contrast to the green limits.
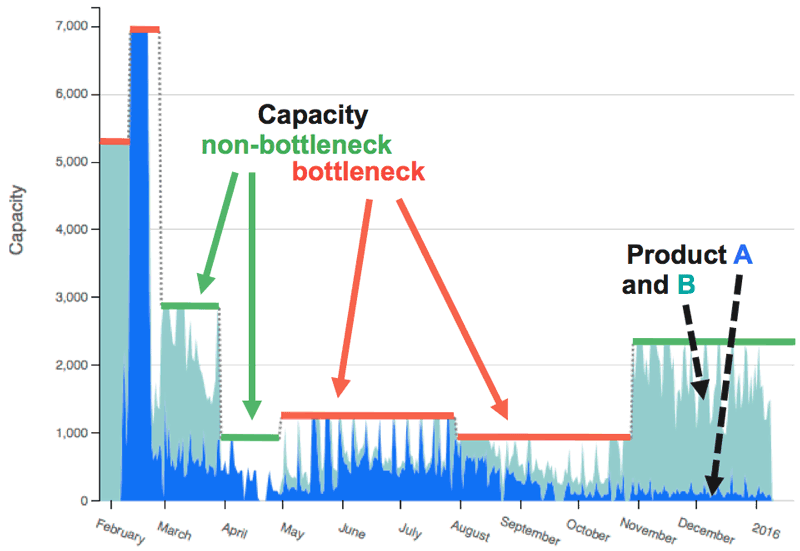
Figure 3: Capacity and utilisation chart over time (red limit: critical, service-level affecting bottleneck).
The simulation uses the obtained policies and runs hundreds of scenarios with different realizations of all stochastic parameters. The result of each scenario incorporates the full complexity of the business environment. This includes specific sequences of processing products at each point in time, dependencies regarding the availability of components, the maximal limit of produced units per day or the maximal “work in progress” (WIP) for a specific product. The different scenario results are aggregated to obtain a plausible range of what the company can expect in the future for each performance indicator of interest. It is straightforward to indicate potential future problems and their correlation on the BOM-tree via colour-coding (Figure 1). This strongly enhances the visibility across the entire supply network, facilitates a targeted problem resolution, and prevents more severe disruptions and variability. Of course, automated alerts can be sent to mobile devices to trigger an exception process.
In summary, the key ingredient for success for these complex projects is the right mixture of innovation and stability — by combining “cutting-edge” and “practice-proven” elements within models, algorithms, software, infrastructure and processes. The “intelligent glue” between these elements originates from both a deep expertise in this area and considerable creativity.
Link:
http://www.research.ibm.com/labs/zurich/business_optimization/
References:
[1] APICS: APICS Dictionary. 14th edition. Chicago, 2013.
[Ut11] Jim Utsler: Taming the supply chain. Interview with M. Parente et al., IBM Systems Magazine, July 2011, 12-15, 2011.
Please contact:
Ulrich Schimpel
IBM Research Zurich, Switzerland











