Position-based cryptography offers new cryptographic methods ensuring that certain tasks can only be performed at a particular geographical position. For example, a country could send a message in such a way that it can only be deciphered at the location of its embassy in another country. Using classical communication, such tasks are impossible to perform. At CWI, we investigate whether position-based cryptography can be achieved if players are allowed to use quantum communication.
Quantum cryptography makes use of the quantum-mechanical behavior of nature for the design and analysis of cryptographic schemes. Its aim is to design cryptographic schemes whose security is guaranteed solely by the laws of nature. This is in sharp contrast to most standard cryptographic schemes, which in principle, can be broken, i.e., when given sufficient computing power. From a theoretical point of view, quantum cryptography offers a beautiful interplay between the mathematics of adversarial behaviour and quantum information theory.
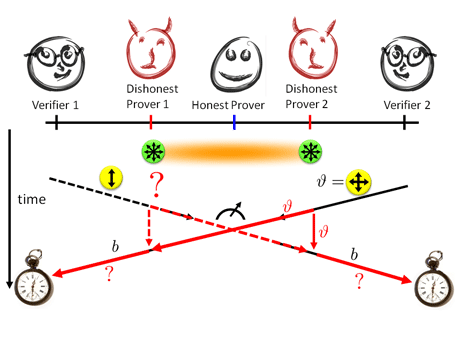
Figure 1: Quantum protocol for position verification in one dimension. (Picture by C. Schaffner with images from Svilen Milev and Victor Zuydweg.)
The best-known application of quantum cryptography is quantum key distribution (QKD). QKD allows two distant parties to securely communicate in a way that cannot be eavesdropped on. The technical requirements to perform QKD protocols are well within reach of today's technology; in fact, QKD devices are currently produced and sold commercially. QKD requires the two involved parties to know and trust each other. In general, however, cryptography is concerned with scenarios where the involved parties want to exchange data without trusting each other. In order to distinguish themselves from an attacker, legitimate players commonly use some form of credential, for example, a digital secret key or biometric data such as a fingerprint. The goal of position-based cryptography is to let the geographical position of a person act as its only credential for accessing secured data and services. This has the important advantage that no digital keys need to be distributed and locally stored, which is often the bottleneck in standard cryptographic solutions and offers opportunities for attacks.
Position-based cryptography has a number of interesting applications. For example, it enables secure communication over an insecure channel without having any pre-shared key, with the guarantee that only a party at a specific location can learn the content of the conversation; think of a military commander who wants to communicate with a base which is surrounded by enemy territory, or a country that wants to send instructions to an embassy in a foreign country. Another application is authenticity verification, where position-based cryptography enables users to verify that a received message originates from a particular geographical position and was not modified during the transmission.
In 2009, it was proven by our collaborators from the University of California in Los Angeles (UCLA) that position-based cryptography is impossible in the classical (non-quantum) world in the setting where colluding opponents control the whole space which is not occupied by honest players. In our latest research article, we investigate whether the impossibility of position-based cryptography can be overcome if we allow the players to use quantum communication.
The outcome of our theoretical investigation demonstrates that the possibility of doing secure position-based cryptography depends on the opponents' capability of sharing entangled quantum states. On the one hand, we show that if the opponents cannot share any entangled quantum state, then secure position-based cryptography is possible. We present a scheme which allows a player, Alice, to convince the other participants in the protocol that she is at a particular geographical position. In contrast, colluding opponents who are not at this position and do not share any entangled quantum state will be detected lying if they claim to be there. Our scheme is very simple and can be implemented with today's QKD hardware. More advanced applications (as outlined above) can be based on our scheme.
On the other hand, we also show that if the opponents are able to share a huge entangled quantum state, then any positioning scheme can be broken and no position-based cryptography is possible at all. In fact, our result shows how colluding opponents can use their entangled state to instantaneously and non-locally perform the honest player's operations and are therefore able to make it appear as if they were at the claimed position.
Our results raise various interesting research questions. For example, it is a formidable technical challenge to store and handle large quantum states. Hence, is secure position-based cryptography possible in the realistic setting where opponents can only handle a limited amount of entangled quantum states? Our investigation has already sparked several follow-up works and first results indicate that there are schemes which remain secure in this bounded-entanglement setting.
Link: http://homepages.cwi.nl/~schaffne/positionbasedqcrypto.php
Please contact:
Christian Schaffner
CWI Amsterdam, Netherlands
Tel: +31 20 592 4236 begin_of_the_skype_highlighting +31 20 592 4236 end_of_the_skype_highlighting
E-mail:










