by Abder Aggoun, Nicolas Beldiceanu, Mats Carlsson and François Fages
Packing items in bins is an old but nevertheless challenging combinatorial problem with numerous applications in industry. We report on an original approach based on constraint programming and rule-based modelling, which has been investigated in the framework of the FP6 ‘specific targeted research project’ Net-WMS (Towards integrating virtual reality and optimization techniques in a new generation of Networked businesses in Warehouse Management Systems under constraints). It has applications in the automotive industry.
Existing Warehouse Management Systems (WMSs) provide advanced features for managing the movement of items within warehouses, but fail to comply with increasing demand for more numerical handling. Generally, WMSs lack optimization functionalities and advanced packing tools for determining how to pack items on a pallet, how many cartons are needed to pack customer items, how to pack pallets in a truck according to stability constraints and delivery route plans, and on a larger scale, how to redesign a storage area, an assembly line or similar.
These combinatorial optimization problems are particular instances of the classical ‘bin packing’ problem, which has contributed to the development of the theory of algorithms and complexity since the early 1970s. The one-dimensional bin packing problem (1BP) is, given N items of possibly different lengths to pack in K bins of a given length capacity, to determine whether a packing solution exists (decision problem), or to determine the minimum value K* of K for which there exists a solution (optimization problem). 1BP directly models simple forms of truck loading or assembly-line design problems. It is however an NP-hard problem, which means that no efficient polynomial-time algorithm exists for solving all instances of this problem, if we admit the conjecture P¹NP.
Two-dimensional (2BP) and three-dimensional (3BP) bin packing problems model many loading problems, respectively by layers or directly in the three dimensional space. These problems contain many variants according to the shapes allowed for the items (squares, rectangles, polytopes etc), and whether or not items may be rotated. All these variants have the same theoretical complexity (NP-hard) as long as a grid of integer coordinates and a finite number of rotations are considered for the packing. The core container loading and pallet loading problems are 3BP problems, but while in bin packing the only objective is to achieve high volumetric use, the real problems require additional constraints.
Rule-based modelling
When packing objects, it is not enough to pack them efficiently. Objects must be packed correctly. For instance, heavy objects must not be piled on top of fragile ones. Boxes must not be left hanging partly unsupported, and so on. Any business that needs to pack something has regulations about how objects may and may not be packed. Unfortunately such knowledge is typically written on paper, in natural language, and is therefore difficult for computers to access.
A key challenge of our work was to come up with a way of encoding this knowledge in a form that a computer can process and use for optimization, and that a human without a computer science degree can read, understand and edit. In this way, not only can the computer come up with packing plans that are space efficient, but also guarantee that such plans obey the business packing regulations.
Most people find it easier to understand or describe a complex design in small pieces than as a monolithic whole. Similarly, in computer science, there exists a formalism for describing knowledge in small pieces: rules. So we decided to define a rule-based formalism, or language, for business packing regulations. Moreover, it must be possible to transform knowledge expressed in our language into executable code for tasks like computing packing plans.

Figure 1. Example of PKML rules defining container loading constraints, gravity and stacking rules
Initially, we aimed at defining a rule-based language specifically for modelling packing problems. Later, we realized that limiting the scope to packing was no advantage, and widened it to include modelling general discrete optimization problems. The resulting language was called Rules2CP, or Rules To Constraint Programming. Rules2CP allows the definition of library modules. We defined such a module tailored to modelling packing problems and named it PKML. It provides a set of generic primitives for use in packing rules.
All optimization software developed in the project is based on the constraint programming approach. The project uses two constraint programming platforms: the open-source Choco Java and the commercial SICStus Prolog platforms. A significant effort went into the development of Rules2CP compilers: one compiler into Java for Choco, and the other into Prolog for SICStus.
We also designed and implemented an alternative approach: to compile a subset of Rules2CP into side-constraints for the ‘geost’ constraint, which is a computational workhorse in our optimization software. The point is to achieve higher efficiency from a tight integration of multiple logical conditions in one single constraint.
Geometrical constraint solving
Constraint programming is a declarative programming paradigm which relies on two components: a constraint component which manages posting and checks satisfiability and entailment of constraints over some fixed computational domain, and a programming component which assembles the constraints of a given problem and expresses search procedures. Because of its capability to handle a great variety of specific requirements, the main technical approach developed by the Net-WMS project to solve packing problems is based on constraint programming, with the aim of making significant advances on the design and implementation of efficient geometrical constraint solvers in this context.
The goal of our research was to provide a flexible geometrical kernel that could directly handle a large class of packing problems. As illustrated in Figure 2 in the context of non-overlapping, this goal has been largely achieved.
Constraint programming was selected since it offered a flexible environment in which to develop such a constraint kernel. More precisely we chose to embed the geometrical kernel within a generic global constraint, named geost, so that it could be used with all standard available constraints of a typical constraint toolkit (Choco and SICStus in our context). The geost constraint is generic in the sense that it can handle the location in space of polymorphic multidimensional objects subject to various geometrical constraints.
A first significant effort in this research was the development of a multi-dimensional sweep-based algorithm that could handle a large class of geometrical constraints in a uniform way. A second significant effort was the development of efficient methods for handling multidimensional non-overlapping constraints. In this context, general necessary conditions were developed, especially cumulative necessary conditions for non-overlapping. Necessary conditions for important special cases (eg pallet loading) were also conceived. Finally, in order to handle the fact that many practical problems consider only a few types of items to place, symmetry-breaking techniques that directly consider non-overlapping were designed.
The specifications of the geometrical kernel developed in this work package were implemented within both the open-source Choco Java library and the SICStus Prolog platform. A third implementation was performed outside the Net-WMS project within the open-source JaCoP constraint library.
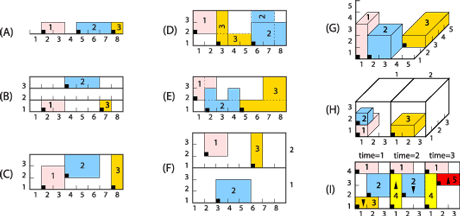
Figure 2: Typical placement problems handled by geost: Case (A) corresponds to a non-overlapping constraint among three segments. The second and third cases (B, C) correspond to a non-overlapping constraint between rectangles. (B) is a special case in which the sizes of all rectangles in the second dimension are equal to 1; this can be interpreted as a machine assignment problem. Case (D) corresponds to a non-overlapping constraint between rectangles where each rectangle can have two orientations. This is achieved by associating with each rectangle two shapes of respective sizes l x h and h x l. Since their orientation is not initially fixed, the included constraint requires that the three rectangles be included within the bounding box defined by the origin's coordinates 1,1 and sizes 8,3. Case (E) corresponds to a non-overlapping constraint between more complex objects where each object is described by a given set of rectangles. Case (F) describes a placement problem in which one must first assign each rectangle to a strip, such that no rectangle overlaps with another assigned to the same strip. Case (G) corresponds to a non-overlapping constraint between orthotopes (the generalization of a rectangle for higher dimension). Case (H) can be interpreted as a non-overlapping constraint between orthotopes that are assigned to the same container. The first dimension corresponds to the identifier of the container, while the next three dimensions are associated with the position of an orthotope inside a container. Case (I) describes a rectangle placement problem over three consecutive time-slots: rectangles assigned to the same time-slot should not overlap in time.
Conclusion
By working on real-size industrial problems that take all business requirements into account, the Net-WMS project has advanced the state of the art in bin packing, constraint programming and modelling languages, making significant progress in the technological transfer toward the end users.
There are still some hard instances however, especially in 3D pallet-loading problems with rotations. In these cases the automatic placement finds sub-optimal solutions – not as good as expert solutions – and we are not aware of alternative automatic methods by which to solve these problems optimally. Current work concerns search strategies, and improvements in the geometrical constraint as well as its generalization to handle hybrid discrete continuous complex shapes.
The technological transfer of Net-WMS components is already ensured by their industrialization by our SME partner KLS OPTIM, as well as by their integration in open-source libraries or in the commercial software of our academic partners EMN, INRIA and SICS. The first version of the KLS Optimization Suite has been released, not only making Net-WMS technology available to the market at the end of the project, but also positioning Net-WMS at the beginning of a new generation of agile supply chain management systems.
Link: http://net-wms.ercim.eu/
Please contact:
François Fages
INRIA Paris-Rocquencourt, France
E-mail:
Abder Aggoun
KLS OPTIM, France
E-mail:
Nicolas Beldiceanu
EMN, France
E-mail:
Mats Carlsson
SICS, Sweden
E-mail:










