by Alain Girault and Hamoudi Kalla
The reliability of a system indicates its continuity of service. It is formally defined as the probability that it will function correctly during a given time interval. With the advent of ubiquitous computing and distributed embedded systems, it is becoming an increasingly crucial aspect. We propose a framework for designing highly reliable real-time systems, thanks to a novel bicriteria (length and reliability) static multiprocessor scheduling heuristic. The first criterion is the schedule's length, which assesses the system's real-time property, while the second is reliability, assessing the system's dependability.
Our new multi-processor static scheduling heuristic, BSH, takes as input two graphs: a data-flow graph (ALG) describing the algorithm of the application, and a graph (ARC) describing the target distributed architecture. Figure 1 (left) shows an example of an algorithm graph: it has nine operations (represented by circles) and eleven data dependences (represented by green arrows). Among the operations, one is a sensor operation (I), one is an actuator operation (O), and the seven others are computations (A to G). On the right is an example of an architecture graph: it has three processors (P1, P2, and P3) and three point-to-point communication links (L1.2, L1.3, and L2.3).
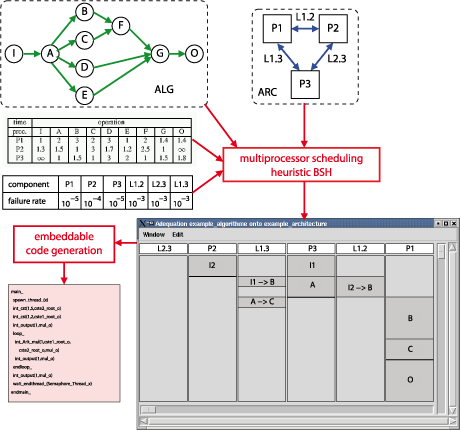
Also given is a table of the worst-case execution time of each operation onto each processor, and the worst-case transmission time of each data dependency onto each communication link. The architecture being heterogeneous, these need not be identical. Below is an example of such a table for the operations of ALG. The infinity sign expresses the fact that the operation I cannot be executed by the processor P3, for instance to account for the requirements of certain dedicated hardware.
Our fault hypothesis is that the hardware components are fail-silent, meaning that a component is either healthy and works well, or is faulty and produces no output at all. Besides, the occurrences of the failures of all hardware components follow a constant parameter Poisson law: according to this model, the reliability of any given hardware component during the interval of time d is equal to e-λd, where l is the failure rate per time unit of the component. The table of the individual failure rates per time unit of all the hardware components is also given. Again, the architecture being heterogeneous, these need not be identical.
From these four inputs, our BSH heuristic distributes the operations of ALG onto the processors of ARC and schedules them statically, as well as the communications induced by these scheduling decisions. The output of the heuristic is therefore a multiprocessor static schedule, from which embeddable code can be generated.
Our contribution is twofold. First, we redefine the framework of bicriteria (length, reliability) scheduling, because the reliability criterion depends intrinsically on the length criterion. This incurs three major drawbacks, common to all bicriteria (length, reliability) scheduling heuristics found in the literature. First, the length criterion overpowers the reliability criterion; second, it is very tricky to control precisely the replication factor of the operations onto the processors, from the beginning to the end of the schedule (in particular, it can cause a 'funnel' effect); and third, the reliability is not a monotonic function of the schedule. To solve this problem, we propose a new criterion to replace reliability, which we call the Global System Failure Rate (GSFR). The GSFR is the failure rate per time unit of the static schedule, seen as if it were a single operation placed onto a single processor.
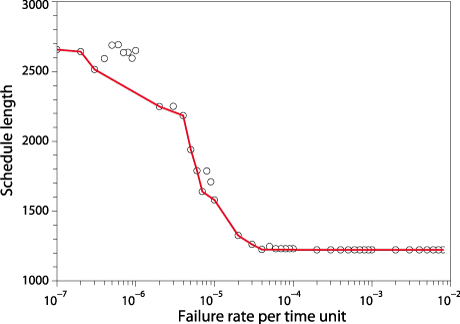
We have conducted extensive simulations that demonstrate that our new bicriteria (length, GSFR) scheduling algorithm BSH avoids the three problems mentioned above. Furthermore, for a given instance of the problem BSH is able to produce a set of non-dominated solutions in the Pareto sense (ie the Pareto curve), from among which the user can choose the solution that best fits the application's requirements. Figure 2 is an example of such a Pareto curve produced on a ten-processor system for an ALG graph of 100 operations.
Link:
Fault-tolerance: http://pop-art.inrialpes.fr/~girault/Projets/FT/
Please contact:
Alain Girault
INRIA Grenoble Rhône-Alpes
Tel: +33 476 61 53 51
E-mail: Alain.Girault![]() inria.fr
inria.fr










